Blogs and Websites

Blogs:

Geometry can be fun!
Teacher Blog Spot
Math Teacher Mambo
Angle Attack
Pinterest

Websites:
Geometry Math Games
Geometry Games
Geometry Games for Kids
Kids Konnect
30 Geometry Games
Basic Skill Practice Games

Post #6

More about angles

Supplementary Angles- Two angles whose sum of measure is 180 degrees (they do not need to be adjacent)
Examples: 140 + 40=180
Complementary Angles- Two angles the sum of whose measures is 90 degrees. Each angle is a compliment of the other. (they do not need to be adjacent)
Example:  60+30= 90
Vertical Angles- Created by intersecting lines which are pairs of angles whose sides are two pairs of opposite rays. VERTICAL ANGLES ARE CONGRUENT.
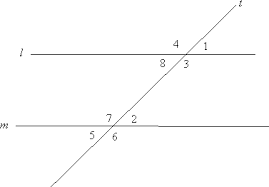Transversals and Angles- Transversal line is any line that intersect a pair of lines in a plane.



Interior angles: <2, <3, <7, <8
Exterior angles: <1, <4, <5, <6
Alternate angles: <2 and <8, <3 and <7
Alternate exterior angles: <1 and <5, <4 and <6
Corresponding angles:
<1 and <2, <4 and <7, <8 and <5, <3 and <6





How to find the sum of the interior angles of a regular n-gon:
n-2(180)

Example:
Decagon
(10-2)(180)
(8)(180)
1440

To get the measurement of each individual interior angle divide the sum of the interior angles by n
1440/10=144



How to find the sum of exterior angles is to then take 180 minus the individual angle and then times by n
180-144=36
36(10)=360

Post #5

Quadrilateral Hierarchy


Trapezoid- quadrilateral with at least one parallel sides 
Parallelogram- a quadrilateral in which each pair of opposite sides is parallel
Rectangle- parallelogram with a right angle
Rhombus- parallelogram with two adjacent sides congruent
Square- a rectangle with two adjacent sides congruent
Kite- a quadrilateral with two adjacent sides congruent and the other two sides also congruent

Post #4

Polygons

Simple curve- a curve that does not cross itself.
Closed curve- a curve that starts and stops at the same point.
Polygon- a simple, closed curve with sides that are line segments.
Convex- simple, closed curve, such that the segment connecting any two points in the interior of the curve is wholly contained in the interior of the curve.
Concave curve- simple, closed curve that is not convex. It is possible for a line segment connecting two interior points to cross outside the interior of the curve.



 
 Interior angles- angle formed by two sides of a polygon with a common vertex
Exterior angles- an angle formed by a side of a polygon and the extension of a contiguous side of the polygon

Triangles

Angles- sum equals 180
Right triangle- contains one right angle
Acute triangle- triangle in which all angles are acute (smaller than 90)
Obtuse triangle- a triangle containing one obtuse (bigger than 90) angle

Sides
Scalene triangle- triangle with no congruent sides
Isosceles triangle- triangle with at least two congruent sides
Equilateral triangle- a triangle with three congruent sides

 

Post #3

Angles

Angles are formed by two rays with the same endpoint
Sides of an angle are formed by the two rays to form an angle
Vertex is the common endpoint of the two rays that form an angle
(it is complimentary to name an angle by its vertex)
Example: <B or <ABC

Types of Angles:
Acute- less than 90 degrees
Right- exactly 90 degree angle
Obtuse- greater than 90 degrees but less than 180 degrees  
Straight- exactly 180 degrees

 Angle Measurement

How to add and subtract angles that have degrees minutes and seconds

    1835' 29"
 + 2255' 41"
    4090' 70"
           +1  -60
   40 91'  10"
   +1   -60         
   4131'  10"

 14       89
  15 29'
-  3 45'
  11 44'

Post #2

Points and Lines

First thing you need to know is about the different types of lines:
Segment- a subset of a line that contains two points of the line and all points between those two points
Ray- a subset of a line that extends forever in one direction
Line- has no thickness and extends forever in two directions

Collinear Points- points that fall on the same line

Intersecting Lines- lines with exactly one point in common

Parallel Lines- coplanar lines thast have no points in common represented as C // D

Post #1

In this weeks class we touched on a little bit of the basics of Geometry. Geometry is is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. There are many different parts of Geometry so when you bring it to your students make sure that you ease them in slow.

Here is a video for teachers that are a little rusty on their Geometry and want a refresher before teaching their students.